Почему в немецком языке число 25 читается как \"пять и двадцать\"?

Почему в немецком языке число 25 читается как \"пять и двадцать\" (\"fünf und zwanzig\"), а не \"двадцать пять\" как в русском, английском и др. (на тот момент мне известных) языках?
Этот вопрос занимал меня с самого начала изучения немецкого.
Ответа у филологов я не нашел.
Когда познакомился с НХ и ее дериватами, тоже решения вопроса не встретил.
Поинтересовался на немецком форуме по аналитической истории и хронологии, но даже там кроме встречного любопытства ничего не нашел.

По ходу дела выяснилось, что есть и другие языки с цифрами в «обратном» порядке, как в немецком (полностью или частично), например: арабский; идиш, датский, голландский, сербский, словенский («клоны» немецкого или испытали его влияние); древнегреческий и древнееврейский (иврит)***.
Последние два языка, кстати, наводят на мысль, что в древности порядок слов в двузначных числительных был-таки «обратным» (замечание Basileus).

Итак, почему в некоторых языках употребляется «обратное» (справа налево) произношение цифр в числах?

Мое решение основано на идее Игоря Грека (псевдоним Игоря Шкурина): римские цифры являются упрощенным графическим представлением пальцев в древней пальцевой системе счета. (Цитаты и рисунки ниже - из статьи Грека ).

Для лучшего понимания в используемых сейчас римских цифрах от 1 до 9 сделаем только одну важную поправку - восстановим первоначальное написание цифры 4, которая сейчас обозначается IV (то есть =5-1), а в древности выглядела IIII, поэтому и цифру 9 будем писать как VIIII, а не как IX (то есть =10-1).
Например, в древнеримском календаре \"parapegma\" 3-4 вв. н.э. при написании чисел 4, 9, 14, 19, 24 и 29 используется четырехкратное повторение символов IIII.

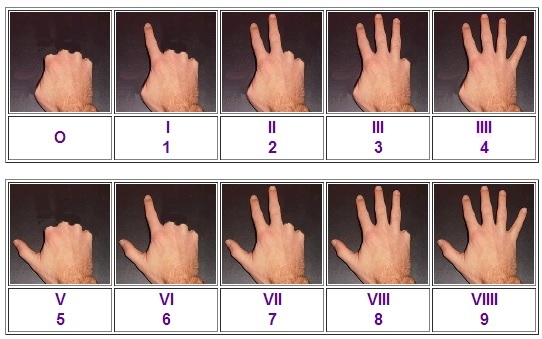
Теперь эти римские цифры можно легко показать на пальцах одной руки, считая большой палец = 5, а остальные = 1, то есть цифре V соответствует отставленный большой палец, а сжатая в кулак рука по форме и значению соответствует цифре \"ноль\" (римляне и греки его не писали, но фактически ноль был). Как видно, написание всех римских цифр является упрощённым изображением фигур, образуемых при счёте на пальцах рук.

Итак, римские цифры до 10 - это легко узнаваемые пиктограммы древнего пальцевого счёта.

правая рука:

На левой руке показываются десятки ...).

левая рука:

Теперь вернемся к вопросу: \"Почему в некоторых языках употребляется «обратное» (справа налево) произношение цифр в числах?“

Я исхожу из аксиомы: \"древние\" люди начинали пользоваться счетом с маленьких чисел.
Им было удобно показывать эти числа на пальцах одной руки (как и сейчас, на самом деле) .
И при этом — говорить: два, три, ...семь *.
И лишь для чисел, больших чем 9 они должны были задействовать вторую руку**, чтобы показать число десятков.
И тогда надо было это число десятков в речи добавлять к уже произнесенному слову — числу единиц.
А для присоединения слова (= «число десятков») стал использоваться обычный соединительный союз \"и\" (в немецком - «und»).
Отсюда и возникла конструкция типа «пять и двадцать».

И только после того, как многозначные числа стали обычной вещью, могла появиться конструкция \"двадцать пять\".

* Конечно, надо было еще догадаться показывать пятерку большим пальцем, а не всеми пятью! Так и теперь математика — удел умных.
** Двенадцатиричный счет по фалангам пальцев руки, а также счет на камушках, узелках и т.п.— это другие истории.
*** Еще есть нюанс с арабским и ивритом — в них пишут и читают справа налево, так что двузначные числа «не плывут против течения». Однако, вряд ли мотивы «обратного» произношения чисел с этим связаны.